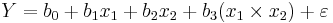Moderation (statistics)

In statistics, moderation occurs when the relationship between two variables depends on a third variable. The third variable is referred to as the moderator variable or simply the moderator ^[1]. The effect of a moderating variable is characterized statistically as an interaction^[1]; that is, a qualitative (e.g., sex, race, class) or quantitative (e.g., level of reward) variable that affects the direction and/or strength of the relation between dependent and independent variables. Specifically within a correlational analysis framework, a moderator is a third variable that affects the zero-order correlation between two other variables. In analysis of variance (ANOVA) terms, a basic moderator effect can be represented as an interaction between a focal independent variable and a factor that specifies the appropriate conditions for its operation (Baron and Kenny, 1986: p. 1174).

Moderation analysis in the behavioral sciences involves the use of linear multiple regression analysis or causal modelling^[1]. To quantify the effect of a moderating variable in multiple regression analyses, regressing random variables Y on X, an additional term is added to the model. This term is the interaction between X and the proposed moderating variable ^[1].

Thus, for a response Y and two variables x₁ and moderating variable x₂,:

$Y = b_0 %2B b_1x_1 %2B b_2x_2 %2B b_3(x_1\times x_2) %2B \varepsilon \,$

In this case, the role of x₂ as a moderating variable is accomplished by evaluating b₃, the parameter estimate for the interaction term^[1]. See linear regression for discussion of statistical evaluation of parameter estimates in regression analyses.

Moderation should not be confused with mediation.

References

^ ^a ^b ^c ^d ^e Cohen, Jacob; Cohen, Patricia; Leona S. Aiken; West, Stephen H. (2003). Applied multiple regression/correlation analysis for the behavioral sciences. Hillsdale, N.J: L. Erlbaum Associates. ISBN 0-8058-2223-2.

Baron, R. M., & Kenny, D. A. (1986). "The moderator-mediator variable distinction in social psychological research: Conceptual, strategic, and statistical considerations." Journal of Personality and Social Psychology, Vol. 51, No. 6, pp. 1173–1182.
Hayes, A. F., & Matthes, J. (2009). "Computational procedures for probing interactions in OLS and logistic regression: SPSS and SAS implementations." Behavior Research Methods, Vol. 41, pp. 924-936.

Statistics

Descriptive statistics

Continuous data

Location	Mean (Arithmetic, Geometric, Harmonic) Median Mode

Dispersion	Range Standard deviation Coefficient of variation Percentile Interquartile range

Shape	Variance Skewness Kurtosis Moments L-moments

Count data

Index of dispersion

Summary tables

Dependence

Statistical graphics

Data collection

Designing studies	Effect size Standard error Statistical power Sample size determination

Survey methodology	Sampling Stratified sampling Opinion poll Questionnaire

Controlled experiment	Design of experiments Randomized experiment Random assignment Replication Blocking Factorial experiment Optimal design

Uncontrolled studies	Natural experiment Quasi-experiment Observational study

Statistical inference

Statistical theory	Sampling distribution Sufficient statistic Meta-analysis

Bayesian inference	Bayesian probability Prior Posterior Credible interval Bayes factor Bayesian estimator Maximum posterior estimator

Frequentist inference	Confidence interval Hypothesis testing Likelihood-ratio

Specific tests	Z-test (normal) Student's t-test F-test Pearson's chi-squared test Wald test Mann–Whitney U Shapiro–Wilk Signed-rank Kolmogorov–Smirnov test

General estimation	Bias Robustness Efficiency Maximum likelihood Method of moments Minimum distance Density estimation

Correlation and regression analysis

Correlation	Pearson product-moment correlation Partial correlation Confounding variable Coefficient of determination

Regression analysis	Errors and residuals Regression model validation Mixed effects models Simultaneous equations models

Linear regression	Simple linear regression Ordinary least squares General linear model Bayesian regression

Non-standard predictors	Nonlinear regression Nonparametric Semiparametric Isotonic Robust

Generalized linear model	Exponential families Logistic (Bernoulli) Binomial Poisson

Partition of variance	Analysis of variance (ANOVA) Analysis of covariance Multivariate ANOVA Degrees of freedom

Categorical, multivariate, time-series, or survival analysis

Categorical data	Cohen's kappa Contingency table Graphical model Log-linear model McNemar's test

Multivariate statistics	Multivariate regression Principal components Factor analysis Cluster analysis Copulas

Time series analysis	Decomposition (Trend, Stationary process) ARMA model ARIMA model Vector autoregression Spectral density estimation

Survival analysis	Survival function Kaplan–Meier Logrank test Failure rate Proportional hazards models Accelerated failure time model

Applications

Biostatistics	Bioinformatics Biometrics Clinical trials & studies Epidemiology Medical statistics

Engineering statistics	Chemometrics Methods engineering Probabilistic design Process & Quality control Reliability System identification

Social statistics	Actuarial science Census Crime statistics Demography Econometrics National accounts Official statistics Population Psychometrics

Spatial statistics	Cartography Environmental statistics Geographic information system Geostatistics Kriging

Category
Portal
Outline
Index

Moderation (statistics)

See also

References